note on the subcortical part of CIFTIs

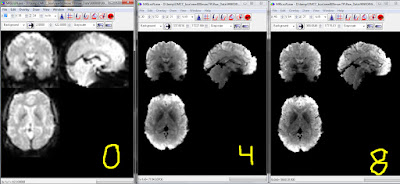
As people working with HCP CIFTI images know, the cortex is represented by (surface) vertices, but subcortical structures as voxels. As I explained before, you can use the wb_command -cifti-separate to make a volumetric NIfTI of a subcortical structure (say AMYGDALA_LEFT). The HCP minimally preprocessing pipelines create the CIFTI versions of each (task, in my case) run and also volumetric NIfTI versions. So my question: is timecourse of a voxel in a subcortical structure the same when taken out of an unpacked CIFTI and a NIfTI? Answer: no.

This screenshot shows the volumetric NIfTI (red stripe),
 AMYGDALA_LEFT via wb_command -cifti-separate (green stripe), and the _AtlasSubcortical_s2.nii.gz image (yellow stripe) for one of our HCP pipeline minimally-processed task fMRI runs.

The _AtlasSubcortical_s2.nii.gz image was created by the pipeline, and looks to be the subcortical (volumetric) part of the CIFTI: the value at this voxel is identical (green and yellow). The value for the voxel in the volumetric NIfTI (red) is a bit different, however.

Note that I don't think this mismatch is an error: parcel-constrained smoothing is done during the HCP pipelines that make the CIFTIs (e.g., Glasser et al. 2013), and I suspect that this smoothing accounts for the different voxel values. However, it's good to be aware of the additional processing: if you're doing a volumetric analysis with HCP-type preprocessing, it matters whether you take the subcortical structures out of the CIFTI or the NIfTI.

an update and some musings on motion regressors

In case you don't follow practiCal fMRI (you should!), his last two posts describe a series of tests exploring whether or not the multiband (AKA simultaneous multi-slice) sequence is especially liable to respiration artifacts: start here, then this one. Read his posts for the details; I think a takeaway for us non-physicists is that the startlingly-strong respiration signal I (and others) have been seeing in multiband sequence timecourses and motion regressors is not from the multiband itself, but rather that respiration and other motion-type signals are a much bigger deal when voxels are small (e.g., 2 mm isotropic).

This week I dove into the literature on motion regression, artifact correction, etc. Hopefully I'll do some research blogging about a few papers, but here I'll muse about one specific question: how many motion regressors should we use (as regressors of no interest) for our task GLMs? 6? 12? 24? This is one of those questions I hadn't realized was a question until running into people using more than 6 motion regressors (the 6 (x,y,z,roll,pitch,yaw) come from the realignment during preprocessing; transformations of these values are used to make the additional regressors).

Using more than 6 motion regressors seems more common in the resting state and functional connectivity literature than for task fMRI (Power et al. 2015, and Bright & Murphy 2015 , for example). I found a few (only a few) task papers mentioning more than 6 motion regressors, such as Johnstone et al. 2006, who mention testing "several alternative covariates of no interest derived from the estimated motion parameters", but they "lent no additional insight or sensitivity", and Lund et al. 2005, who concluded that including 24 regressors was better than none.

Out of curiosity, we ran a person through an afni TENT GLM (FIR model) using 6 (left) and 24 (right) motion regressors. This is a simple control analysis: all trials from two runs (one in blue, the other orange), averaging coefficients within my favorite left motor Gordon parcel 45 (there were button pushes in the trials). It's hard to tell the difference between the model with 6 and 24 regressors: both are similar and reasonable; at least in this test, the extra regressors didn't have much of an effect.

My thinking is that sticking with the usual practice of 6 regressors of no interest is sensible for task fMRI: adding regressors of no interest uses more degrees of freedom in the model, risks compounding the influence of task-linked motion, and hasn't been shown superior. But any other opinions or experiences?

multiband acquisition sequence testing: timecourses 2

In a previous post I showed timecourses from the same person, doing the HCP MOTOR task, collected with a multiband 4 and a multiband 8 sequence (see previous posts for details). We ran another test person ("999010") through the same task, with the same two sequences (but not the MB0 control).

This plot shows the average activation (post-preprocessing) in the same SMmouthL Gordon parcel as before, but with the respiration recording as background (light blue), instead of the motion regressors. As before, since this is a mouth parcel, the activation should be strongest to the green "tongue" movement blocks. The respiration recording, events, and average activation are temporally aligned to the actual TR (x-axis), not shifted to account for the hemodynamic delay.

It is clear in both the MB8 and MB4 recordings that task activation is present, but it is perhaps a bit clearer with MB4. The little "jiggles" in the timecourse are present in all four runs, and look to be related to respiration, though not perfectly aligned with respiration. We're switching our ongoing MB8 imaging study to MB4 in the hopes of improving signal-to-noise, but respiration-related effects still look to be prominent in the MB4 BOLD, so dealing with them is an ongoing project.

respiration and movement: more experiences

Annika Linke, a postdoc at SDSU, contacted me, reporting that she's also seen oscillations in multiband acquisitions, with a Siemens Trio and Prisma, plus a GE Discovery. She kindly sent examples of her findings, and allowed me to share and describe a few of them here. More examples can be downloaded here and here.

Annika ran a multiband 8 sequence on a GE 3T Discovery MR750 scanner (UCSD CFMRI; TR = 800 msec, mb_factor 8, 32 channel head coil, 2 x 2 x 2 mm voxels; AP - PA encoding directions), and also saw prominent oscillations in the motion regressors, linked to respiration:

The subject was sleeping in this scan, and periodically stopped breathing. The movement in the motion regressors stopped and starts with the abnormal breathing periods, very similar to the traces from the purposeful breath-holding experiment we ran. I was also struck by the size of the oscillations in the movement regressors: somewhere between 0.5 and 1 mm, which neatly matches the size of the larger oscillations we've seen. Annika has results for an awake adult and toddlers, all of whom show oscillations (particularly in the A-P (y) and I-S (z) axes); see this pdf. These comparisons suggest the oscillation magnitude is not directly related to participant weight: the toddler and adult magnitudes are similar, though toddlers of course are smaller and have a faster respiration rate.

Here are some motion regressors Annika collected on a different scanner (Siemens 3T Prisma at Robarts Research Institute, Western University; CMRR release 10b, VD13D, 64 channel head coil, 3 x 3 x 3 mm voxels), at different MB factors. The oscillation is in all runs, though lowest amplitude with MB1.  

Finally, here's a set of motion regressors collected on a Trio at MB2 (ipat2 acceleration, 2 mm voxels, TR=1300 msec, AP/PA phase encoding directions, Robarts Research Institute, Western University). Each subplot is a run from a different person. All again have oscillations mostly in the y and z directions, though the magnitude is less than the MB8 plots above.

Annika's results make it clear that the magnitude of the oscillations in the motion regressors is not due to some weird fluke with our scanner, but rather some aspect of the multiband sequences (or some related factor, such as reconstruction, etc.); hopefully these additional examples will help us understand what's going on.

multiband acquisition sequence testing: respiration

This post is about the relationship between respiration and the movement regressors that we've found in our multiband acquisition sequence testing; see this post for an introduction; this post for examples of activation timecourses, and this post for examples from different people and tasks.

During our acquisition testing session, our participant did breath-holding for one set of MB8 runs, instead of the hand/foot/tongue movements, using the task cues to pace his breath-holding periods.

The light blue line is the respiration recording from a chest belt, with the six columns of the movement regressors overlaid, and the colored blocks at the bottom indicating task cues (as in the plots in the previous posts). Note that the time alignment is not totally perfect for the respiration trace: our system records respiration longer than the fMRI run, and I can't (yet) extract the run onset and offset signals. I aligned the traces using the breath-holding periods, but won't guarantee the timing is to-the-second perfect.

Regardless, the breath-holding periods are clear, and it's also clear that the oscillations in the movement regressors are related to the breathing. The start and stop of motion is also visible in a movie of the raw (before preprocessing) image, which can be seen here: the brain "jitters", then stops, then jitters, then stops (the movie is of the PA MOTORbreath run).

Here are two traces from the MOTOR task runs; plots for the rest of the runs can be downloaded here. The oscillations in the movement regressors is clearly closely linked to the respiration.

Interestingly, the biggest oscillation in the movement regressors here is split between several columns (dark blue, medium blue, light red), where before it was confined to one column (same participant as here); perhaps the head position or packing varied a bit?

Again, it's not new to note that fMRI is affected by breathing. What does seem different is the magnitude of the effect: these scans seem more affected, both in the motion regressors and (more importantly for us, the BOLD). For example, this last set of images shows the movement regressors for the MB0 (no multiband) runs from or test session, and a person from a different MB0 dataset ("BSF117"; a different scanner). A few blips are visible, but smaller. The MB8 and BSF117 examples below were downsampled to match the MB0 TR; note that these are the same MB8 movement regressors as above: after downsampling the oscillations no longer tightly match the respiration, but are still more prominent than the others.

multiband acquisition sequence testing: timecourses

This post is about timecourses found in our multiband acquisition sequence testing; see the previous post for the introduction and following for respiration recordings. The HCP MOTOR task is good for these tests since the expected effects are clear: left hand movement should cause strong activation in right M1, etc. The plots for one ROI are in this post; plots for hand and visual parcels in each hemisphere are in this pdf. Note also that averaging voxel timecourses within parcels somewhat corrects for the different voxel size (and presumably signal) associated with each acquisition: the number of voxels in each parcel for each acquisition is given in the plot titles (e.g., for parcel 3 below, there are 275 voxels at MB8, 180 at MB4, and 73 at MB0).

The black line in these plots is the average timecourse for Gordon parcel 3, part of the SMmouthL community, at our three test acquisitions (timecourses extracted from preprocessed images). This  parcel should be most responsive to the tongue-moving task (green blocks). Task-related activity is indeed apparent with all sequences, but superimposed oscillations are also apparent (which sort of look like the HCP data), particularly at MB8. By eye, it's harder to separate the task-related activation with the MB8 sequence, which is worrying for our event-related analyses.

 

Not wanting to visually mistake the difference in sampling frequency for a smoother signal, I resampled the MB8 timeseries to match the MB4 frequency, shown below (second section of the pdf). Downsampling does reduce the visual difference between the signals, but by eye, MB4 generally still has a clearer signal.

The magnitude of the oscillation varies with acquisition: greatest in MB8, then MB4, and smallest in MB0. The movement regressors (from the HCP pipelines for MB8 and MB4, from SPM for MB0) are shown in light colors on the plots (first column green, second blue, third pink). The oscillation in the activation timecourses looks to be clearly related to the oscillation in the movement lines, which in turn is related to respiration (examples of respiration recordings in the next post, as well as this previous post). An effect of respiration on BOLD is expected and known for a long time; the problem here is that the effect seems larger in magnitude, and perhaps higher in MB8 than MB4. By my eye, the magnitude of the oscillation doesn't appear totally consistent effect across the brain, making it potentially harder to model out post-processing; but this variation is simply my impression so far.

I'm happy to share volumes, etc. if any of you have ideas for additional analyses or want to explore further, and appreciate any thoughts. The preprocessing pipelines also generated surface versions of the files, which I am unlikely to be able to look at any time soon.

multiband acquisition sequence testing: introduction

In the previous couple of posts I shared some strange-looking motion regression curves, which turned out to be related to respiration. I also posted examples of average voxel timecourses which I've been looking at to get a feel for the task-related signal in these images, and how it might be impacted by the respiration-related oscillations. Task-related signal is of primary importance to us (e.g., MVPA and FIR analyses), and ideally analysis of single events. So, everything here is through that lens; implications for resting state, functional connectivity analyses, etc. are likely very different, and I'm not going to speculate on that at all.

We've done a lot of analyses this week, and people have been kind enough to share some of their data and thoughts. This is a lot of material and fairly preliminary, but I think will be of great interest to people using multiband sequences and/or HCP data, so I'll put a few posts together, rather than trying to fit everything into one.

Last Sunday we ran a series of test scans, using as participant the lab member with the most prominent oscillations (examples of which are shown here), and the HCP MOTOR task. This task is short (just over 3.5 minutes long), and has blocks of right or left hand movement, right or left foot movement, and tongue movement. I showed example timecourses from the HCP in the previous post; the graphs from our test runs (see this post) are the same, except that I color-coded the task blocks by body type for easier visibility.

We ran three main test sequences, plus a few variations. Acquisition details are below the fold. The three main sequences were:

• MB8: The same multiband 8 sequence we've been using (described here), except with LeakBlock enabled. TR = 800 msec, acquired voxels 2 x 2 x 2 mm.
• MB4: A new (for us) multiband 4 sequence. TR = 1200 msec, acquired voxels 2.4 x 2.4 x 2.4 mm.
• MB0: A control, non-multiband sequence, the ep2d_bold built-in scanner sequence.TR = 2500 msec, acquired voxels 4 x 4 x 4 mm.

Preprocessing was through the HCP pipelines for the multiband sequences, through SPM12 for the control (realignment and spatial normalization; voxels resampled to 3x3x3); motion regressors plotted (here) are as generated by those programs. I generated voxel timecourses as described before, using afni and the Gordon parcellation for ROIs. We have respiration belt recordings for the multiband sequences, but not for the control.

The functional images we collected with the multiband acquisitions are beautiful. The screenshot above shows a frame from an AP run of each type (the second left-hand movement block, to be precise), before (top) and after (bottom) preprocessing. The MB8 functional images practically look like anatomical images, there's so much detail.

The next few posts will get into the respiration and activity timecourses we found in each.

acquisition details for MB4 and MB0 below the jump; see the previous post for MB8.

more motion and activation plotting

After my initial "what is this?" post I've become convinced that the oscillations are due to respiration, both from my own data and others' reports. I'll leave it to the physicists to understand why the patterns are especially prominent in these sequences, but I've been trying to understand their impact for our work: we're collecting task data and want to do event-related and FIR analyses. Is the oscillation something superimposed on (but independent of) our real signal such that we can "ignore" or process it out (maybe with signal separation techniques such FIX ICA) after image collection, or is our event-related BOLD getting lost, and we should change the acquisition parameters?

These images show some of the plots I've been playing with to try evaluating those questions, using HCP data for comparison. The x-axis is frame number, with thick vertical grey lines marking one-minute intervals and thin vertical grey lines marking 30-second intervals. The left-side y-axis is translation in mm (from the Movement_Regressors.txt file), while the right-side y-axis is the average BOLD of the voxels in each parcel (which I generated via afni; details below; these are the minimally preprocessed images). Note that the left y-axis (translation) is fixed in all graphs while the right-side axis (activation) varies.

The first three columns of Movement_Regressors.txt are plotted in light green, light blue, and light red (in that order), with the average activation overlaid in black (right-side axis). The dark blue line that tracks the activation is a lowess smooth. I generated these plots for four HCP people, in each of four Gordon parcels (4, 41, 45, 201), and for six task runs (MOTOR, GAMBLING, and EMOTION, RL and LR of each). I chose those task runs because they all involve hand motion, blocked (MOTOR) or as event responses (GAMBLING and EMOTION). The block or button-push time is shown in the graphs as little tick marks along the x-axis, with R and L marking the right and left-hand block onsets for MOTOR. I picked four parcels of similar size; 45 is in the left-hemisphere and 201 in the right-hemisphere SMhand communities, and should show strong hand-motion-related activation.

Plots for all four people, runs, and parcels are in this pdf, with two sets copied in here. These are plots for the four parcels, the MOTOR_RL run only. The purple lines show when we expect hand-motion task activation to be strongest for parcels 45 and 201, and it is, particularly in the smoothed line (good, signal!). The oscillation is also clearly visible, and related (by my eye, at least) to the pattern in the motion regressors. There are also spikes, some of which I marked with red dots. It's a bit hard to see in these plots, but these spikes strike me as aligned to jags in the motion regressor lines (and presumably, respiration).

Looking at a lot of these plots makes me understand why I've had trouble (in the other dataset as well) with single-TR and short temporal-compression analyses (e.g., averaging 4 or 5 TRs after an event): I'm picking up too much of the oscillation. Signal clearly is present here, but trying to detect it for single (or short) events is proving tricky.

(example afni command after the jump)

that's motion? respiration

In the previous post I showed some motion regressors with very regular oscillations. Several of you pointed towards respiration, and I was able today to extract the signal from a respiration belt for a couple of runs. The respiration signal (black line plots) is not perfectly temporally aligned to the movement regressors, but close enough to convince me that respiration is driving the oscillation. We're still looking into various acquisition details for why it is so prominent in this dataset; I am certainly not an MR physicist, but will summarize when we figure something out.

that's motion?

While my blogging has unfortunately been sparse lately, I've still been doing lots of fMRI analysis and MVPA! One project I'm currently involved with is just starting to collect high spatial (voxels acquired at 2x2x2 mm) and temporal (TR=800 msec) resolution task fMRI data using a simultaneous multi-slice (SMS) EPI on a Siemens Prisma 3T scanner (details below the fold). We've been looking closely at participant motion and signal quality, and trying various control analyses (button pushes detected in motor areas, task vs. rest, etc.).

UPDATE: This pattern is related to respiration.

Some of the participants have an oscillation in the movement regressors, and I would love to get your impressions of the pattern. Below are two runs (encoding directions AP and PA) of a task for the participant with the most striking oscillation. Plotted are the six columns (translation in blue, rotation in pink) generated by our implementation of the HCP processing pipelines (the Movement_Regressors.txt file, to be precise; MCFLIRT produces a nearly identical set of values). Acquisition frames are along the x-axis, with vertical lines marking 1 minute intervals (these runs are a bit more than 12 minutes long), and short tick marks indicating event onsets (the events are in three blocks).

The overall motion is quite small: less than a mm over each run, well under the 2 mm isotropic voxel size. But the second column (blue below) has a very clear oscillation, that strikes me as too regular to be physiological in origin. Below are the same values again, but just the translation columns, zoomed-in.

This movement is not a simple bug in the preprocessing, but is visible in the raw (converted to NIfTI and defaced, but not motion-corrected, spatially normalized, or anything else) image (click here to see a movie of 08's Pro1 run). It's also in the voxel intensities. The graph below has the same column 2 translation values as the Pro1 graph above, with the average frame-to-frame intensity of a 1900-voxel box-shaped ROI I put in the frontal lobe superimposed in pink. The two curves clearly track pretty well.

I've never seen movement like this in non-SMS EPI datasets, and its regularity makes me suspect that it's related to the acquisition somehow. I'm certainly not a physicist, so very much would appreciate any insights, or if you've encountered similar movement.

The person whose images are shown in this post has the largest and most regular oscillation of any person we've scanned yet (around 8 people); check below the fold for a few more examples, along with details of the acquisition sequence.

resampling images with afni 3dresample

This is the third post showing how to resample an image: I first covered SPM, then wb_command. afni's 3dresample command is the shortest version yet. I highly suggest you verify that the resampling worked regardless of the method you choose; the best way I know of is simply visually checking landmarks, as described at the end of the SPM post.

The setup is the same as the previous examples:

• inImage.nii.gz is the image you want to resample (for example, the 1x1x1 mm anatomical image)
• matchImage.nii.gz is the image with the dimensions you want the output image to have - what inImage should be transformed to match (for example, the 3x3x3 mm functional image)
• outImage.nii.gz is the new image that will be written: inImage resampled to match matchImage.

The command just lists those three files, with the proper flags:

 3dresample -master matchImage.nii.gz -prefix outImage.nii.gz -inset inImage.nii.gz  

Not being especially linux-savvy (afni does not play nice with Windows, so I run it in NeuroDebian), I sometimes get stuck with path issues when running afni commands. When in doubt, navigate to the directory in which the afni command programs (3dresample, in this case) are located, and execute the commands from that directory, typing./ at the start of the command. You can specify the full paths to images if needed; the example command above assumes 3dresample is on the path and the images are in the directory from which the command is typed. If you're using NeuroDebian, you can add afni to the session's path by typing . /etc/afni/afni.sh at the command prompt before trying any afni commands.

"Classification Based Hypothesis Testing in Neuroscience", permuting

My previous post described the below-chance classification part of a recent paper by Jamalabadi et. al; this post will get into the parts on statistical inference and permutation testing.

First, I fully agree with Jamalabadi et. al that MVPA classification accuracy (or CCR, "correct classification rate", as they call it) alone is not sufficient for estimating effect size or establishing significance. As they point out, higher accuracy is better, but it can only be directly compared within a dataset: the number of examples, classifier, cross-validation scheme, etc. all influence whether or not a particular accuracy is "good". Concretely, it is very shaky to interpret a study as "better" if it classified at 84% while a different dataset in a different study classified at 76%; if, however, you find that changing the scaling of a dataset improves classification (of a single dataset) from 76 to 84%, you'd be more justified in calling it an improvement.

The classification accuracy is not totally meaningless, but you need something to compare it to for statistical inference. As Jamalabadi et. al put it (and I've also long advocated), "We propose that MVPA results should be reported in terms of P values, which are estimated using randomization tests."{Aside: I think it's ok to use parametric tests for group-level inference in particular cases and after checking their assumptions, but prefer permutation tests and think they can provide stronger evidence.}

But there's one part of the paper I do not agree with, and that's their discussion of the prevalence of highly non-normal null distributions. The figure at left is Figure 5 from the paper, and are very skewed and non-normal null distributions resulting from classifying simulated datasets in different ways (chance should be 0.5). They show quite a few skewed null distributions from different datasets in the paper, and in the Discussion state that, "For classification with cross-validation in typical life-science data, i.e., small sample size data holding small effects, the distribution of classification rates is neither normal nor binomial."

However, I am accustomed to seeing approximately normal null distributions with MVPA, even in situations with very small effects and sample sizes. For example, below are null distributions (light blue) from eight simulated datasets. Each dataset was created to have 20 people, each with 4 runs of imaging data, each of which has 10 examples of each of 2 classes, and a single 50-voxel ROI. I generated the "voxel" values from a standard normal, with varying amounts of bias added to the examples of one class to allow classification. Classification was with leave-one-run-out cross-validation within each person, then averaging across the runs for the group-level accuracy; 1000 label rearrangements for the permutation test, following a dataset-wise scheme, averaging across subjects like in this demo.

The reddish line in each plot is the accuracy of the true-labeled dataset, which you can see increases from left to right across the simulated datasets, from 0.51 (barely above chance) to 0.83 (well above chance). The permutation test (perm. p) becomes more significant as the accuracy increases, since the true-labeled accuracy shifts to the right of the null distribution.

Note however, that the null distributions are nearly the same and approximately normal for all eight datasets. This is sensible: while the amount of signal in the simulated datasets increases, they all have the same number of examples, participants, classification algorithm (linear SVM, c=1), and cross-validation scheme. The different amounts of signal don't affect the permutation datasets: since the labels were randomized (within each subject and run), all permutation datasets are non-informative, and so produce similar null distributions. The null distributions above are for the group level (with the same dataset-wise permutation relabelings used within each person); I typically see more variability in individual null distributions, but with still approximate normality.

I suspect that the skewed null distributions obtained by Jamalabadi et. al are due either to the way in which the labels were permuted (particularly, that they might not have followed a dataset-wise scheme), or to the way the datasets were generated (which can have a big impact). Regardless, I have never seen as highly-skewed null distributions in real data as those reported by Jamalabadi et. al.



Jamalabadi H, Alizadeh S, Schönauer M, Leibold C, & Gais S (2016). Classification based hypothesis testing in neuroscience: Below-chance level classification rates and overlooked statistical properties of linear parametric classifiers. Human brain mapping, 37 (5), 1842-55 PMID: 27015748

"Classification Based Hypothesis Testing in Neuroscience"

There's a lot of interesting MVPA methodology in a recent paper by Jamalabadi et. al, with the long (but descriptive) title "Classification Based Hypothesis Testing in Neuroscience: Below-Chance Level Classification Rates and Overlooked Statistical Properties of Linear Parametric Classifiers". I'll focus on the below-chance classification part here, and hopefully get to the permutation testing parts in detail in another post; for a very short version, I have no problem at all with their advice to report p-values and null distributions from permutation tests to evaluate significance, and agree that accuracy alone is not sufficient, but they have some very oddly-shaped null distributions, which make me wonder about their permutation scheme.

Anyway, the below-chance discussion is mostly in the section "Classification Rates Below the Level Expected for Chance" and Figure 3, with proofs in the appendices. Jamalabadi et. al set up a series of artificial datasets, designed to have differing amounts of signal and number of examples. They get many below-chance accuracies when "sample size and estimated effect size is low", which they attribute to "dependence on the subsample means":

 "Thus, if the test mean is a little above the sample mean, the training mean must be a little below and vice versa. If the means of both classes are very similar, the difference of the training means must necessarily have a different sign than the difference of the test means. This effect does not average out across folds, ....."

They use Figure 3 to illustrate this dependence in a toy dataset. That figure is really too small to see online, so here's a version I made (R code after the jump if you want to experiment).

This is a toy dataset with two classes (red and blue), 12 examples of each class. The red class is from a normal distribution with mean 0.1, the blue, a normal distribution with mean -0.1. The full dataset (at left) shows a very small difference between the classes: the mean of the the blue class is a bit to the left of the mean of the red class (top row triangles); the line separates the two means.

Following Jamalabadi et. al's Figure 3, I then did a three-fold cross-validation, leaving out four examples each time. One of the folds is shown in the right image above; the four left-out examples in each class are crossed out with black x. The diamonds are the mean of the training set (the eight not-crossed-out examples in each class). The crossed diamonds are the means of the test set (the four crossed-out examples in each class): and they are flipped: the blue mean is on the red side, and the red mean on the blue side. Looking at the position of the examples, all of the examples in the blue test set will be classified wrong, and all but one of the red: accuracy of 1/8, which is well below chance.

This is the "dependence on subsample means": pulling out the test set shifts the means of the remaining examples (training set) in the other direction, making performance worse (in the example above, the training set means are further from zero than the full dataset). This won't matter much if the two classes are very distinct, but can have a strong impact when they're similar (small effect size), like in the example (and many neuroimaging datasets).

Is this an explanation for below-chance classification? Yes, I think it could be. It certainly fits well with my observations that below-chance results tend to occur when power is low, and should not be interpreted as anti-learning, but rather of poor performance. My advice for now remains the same: if you see below-chance classification, troubleshoot and try to boost power, but I think we now have more understanding of how below-chance performance can happen.


Jamalabadi H, Alizadeh S, Schönauer M, Leibold C, & Gais S (2016). Classification based hypothesis testing in neuroscience: Below-chance level classification rates and overlooked statistical properties of linear parametric classifiers. Human brain mapping, 37 (5), 1842-55 PMID: 27015748

follow the jump for the R code to create the image above

pointer: PRNI 2016 paper submission deadline next week

The paper submission deadline for Pattern Recognition in Neuroimaging (PRNI) 2016 has been extended to 24 March, so be sure to get your manuscript in! For those of you with a psychology-type background, note that papers accepted to PRNI are cite-able, peer-reviewed publications, and will be published by IEEE.

This workshop is a great way to meet people interested in MVPA methods; not just SVMs and fMRI (though that's present), but also MEG, EEG, structural MRI, Bayesian methods, model interpretation, etc, etc. PRNI is in Trento, Italy this year, with a shuttle bus to Geneva, Switzerland for those attending OHBM as well (PRNI is held immediately prior to OHBM).

distance metrics: what do we mean by "similar"?

There are many ways of quantifying the distance (aka similarity) between timecourses (or any numerical vector), and distance metrics sometimes vary quite a bit in which properties they use to quantify similarity. As usual, it's not that one metric is "better" than another, it's that you need to think about what constitutes "similar" and "different" for a particular project, and pick a metric that captures those characteristics.

I find it easiest to understand the properties of different metrics by seeing how they sort simple timecourses. This example is adapted from Chapter 8 (Figure 8.1 and Table 8.1) of H. Charles Romesburg's Cluster Analysis for Researchers. This is a highly readable book, and I highly recommend it as a reference for distance metrics (he covers many more than I do here), clustering, tree methods, etc. The computer program sections are dated, but such a minor part of the text that it's not a problem.

Here are the examples we'll be measuring the distance between (similarity of). To make it concrete, you could imagine these are the timecourses of five voxels, each measured at four timepoints. The first four timeseries are the examples from Romesburg's Figure 8.1. Timeseries 1 (black line) is the "baseline"; 2 (blue line) is the same shape as 1, but shifted up 15 units; 3 (red line) is baseline * 2; and 4 (green line) is the mirror image of the baseline (line 1, reflected across y = 20). I added line 5 (grey), to have a similar mean y as baseline, but closer in shape to line 4.

Here are the values for the same five lines:

 data1 <- c(20,40,25,30);   
 data2 <- c(35,55,40,45);   
 data3 <- c(40,80,50,60);   
 data4 <- c(20, 0,15,10); # first four from Romesburg Table 8.1  
 data5 <- c(30,20,26,20); # and another line  

Which lines are most similar? Three metrics.

If we measure with Euclidean distance, lines 1 and 5 are closest. The little tree at right is built from the distance matrix printed below, using the R code that follows. I used R's built-in function to calculate the Euclidean distance between each pair of lines, putting the results into tbl in the format needed by hclust.

Euclidean distance pretty much sorts the timecourses by their mean y: 1 is most similar (smallest distance) to 5, next-closest to 2, then 4, then 3 (read these distances from the first column in the table at right).

Thinking of these as fMRI timecourses, Euclidean distance pretty much ignores the "shape" of the lines (voxels): 1 and 5 are closest, even though voxel 1 has "more BOLD" at timepoint 2 and voxel 5 has "less BOLD" at timepoint 2. Likewise, voxel 1 is closer to voxel 4 (its mirror image) than to voxel 3, though I think most people would consider timecourses 1 and 3 more "similar" than 1 and 4.

 tbl <- array(NA, c(5,5));   
 tbl[1,1] <- dist(rbind(data1, data1), method='euclidean');   
 tbl[2,1] <- dist(rbind(data1, data2), method='euclidean');   
 .... the other table cells ....
 tbl[5,5] <- dist(rbind(data5, data5), method='euclidean');   
 plot(hclust(as.dist(tbl)), xlab="", ylab="", sub="", main="euclidean distance"); # simple tree  

Pearson correlation sorts the timecourses very differently than Euclidean distance.

Here's the tree and table for the same five timecourses, using 1-Pearson correlation as the distance metric. Now, lines 2 and 3 are considered exactly the same (correlation 1, distance 0) as line 1; in Romesburg's phrasing, Pearson correlation is "wholly insensitive" to additive and proportional translations. Consistently, lines 4 and 5 (the "downward pointing" shapes) are grouped together, while line 4 (the mirror image) is maximally dissimilar to line 1.

So, Pearson correlation may be suitable if you're more interested in shape than magnitude. In the fMRI context, we could say that correlation considers timecourses that go up and down together as similar, ignoring overall BOLD. If you care that one voxel's timecourse has higher BOLD than another (here, like 2 or 3 being higher than 1), you don't want to use Pearson correlation.

 tbl <- array(NA, c(5,5));  
 tbl[1,1] <- cor(data1, data1);  # method="pearson" is default  
 tbl[2,1] <- cor(data1, data2);  
 tbl[3,1] <- cor(data1, data3);   
 .... the other table cells ....
 tbl[5,5] <- cor(data5, data5);   
 plot(hclust(as.dist(1-tbl)), xlab="", ylab="", sub="", main="1 - Pearson correlation");   

 The coefficient of shape difference metric (page 99 in Romesburg) mixes a bit of the properties of
Euclidean distance and Pearson correlation: it ignores additive translations, but is sensitive to proportional translations.

As seen here, like correlation, the coefficient of shape difference considers lines 1 and 2 identical (maximally similar), but unlike correlation, line 3 is not considered identical to line 1. Like Euclidean distance, the coefficient of shape difference considers lines 3 and 4 farther apart than any other pair of lines (correlation listed 1, 2, and 3 as all equally far from line 4).

I didn't find the coefficient in a built-in R function, but its equation (8.3 in Romesburg) is very simple to implement, as in the code below.

I've tried using the coefficient of shape difference in a few analyses, as its property of being sensitive to proportional translations more closely matches my intuitive understanding of "similar" timecourses. I haven't used it in any published analyses yet, as Pearson correlation has done better. But it certainly seems worth considering.

 # coefficient of shape difference, page 99 of Romesburg  
 get.dist <- function(dataA, dataB) {  
  if (length(dataA) != length(dataB)) { stop("length(dataA) != length(dataB)"); }  
  n <- length(dataA); # number of dimensions  
  d <- sqrt((n/(n-1))*(sum((dataA-dataB)^2)/n - ((1/(n^2))*(sum(dataA) - sum(dataB))^2)));   
    
  return(d);  
 }  
   
 tbl <- array(NA, c(5,5)); # tbl <- array(NA, c(4,4)); #  
 tbl[1,1] <- get.dist(data1, data1); 
.... the other table cells ....
 tbl[5,5] <- get.dist(data5, data5);   
 plot(hclust(as.dist(tbl)), xlab="", ylab="", sub="", main="coeff of shape diff");  

These three ways of measuring the similarity (distance) between timecourses are certainly not the only metrics, but I hope it's clear from just these three that the metric matters; they're not interchangeable.

R demo: specifying side-by-side boxplots in base R

This post has the base R code (pasted after the jump below, and available here) to produce the boxplot graphs shown at right.

Why base R graphics? I certainly have nothing against ggplot2, lattice, or other graphics packages, and  used them more in the past. I've found it easier, though (as in the demo code), to specify the values and location for each boxplot instead of generating complex conditioning statements. This may be a bit of the opposite of the logic of the Grammar of Graphics, but oh well.

yep, it's worth the time to publish code

I have a paper that's getting close to being published in PLOSone. After review, but prior to publication, they require you to not only agree in principle to sharing the dataset, but that it actually be shared. This can be tricky with neuroimaging datasets (size, privacy, etc.), but is of course critically important. It's easy to procrastinate on putting in the time necessary to make the datasets and associated code public; and easy to be annoyed at PLOS for requiring sharing to be set up prior to publication, despite appreciating that such a policy is highly beneficial.

As you can guess from the post title, in the process of cleaning up the code and files for uploading to the OSF, I found a coding bug. (There can't be many more horrible feelings as a scientist than finding a bug in the code for a paper that's already been accepted!) The bug was that when calculating the accuracy across the cross-validation folds, one of the fold's accuracies was omitted. Thankfully, this was a 15-fold cross-validation, so fixing the code so that the mean is calculated over all 15 folds instead of just 14 made only a minuscule difference in the final results, nothing that changed any interpretations.

Thankfully, since the paper is not yet published, it was simple to correct the relevant table. But had I waited to prepare the code for publishing until after the paper had been published (or not reviewed the code at all), I would not have caught the error. Releasing the code necessary to create particular figures and tables is a less complicated undertaking than designing fully reproducible analyses, such as what Russ Poldrack's group is working on, but still nontrivial, in terms of both effort and benefits.

How to avoid this happening again? A practical step might be to do the "code clean up" step as soon as a manuscript goes under review: organize the scripts, batch files, whatever, that generated each figure and table in the manuscript, and, after reviewing them yourself, have a colleague spend a few hours looking them over and confirming that they run and are sensible. In my experience, it's easy for results to become disassociated from how they were generated (e.g., figures pasted into a powerpoint file), and so for bugs to persist undetected (or errors, such as a 2-voxel radius searchlight map being labeled as from a 3-voxel radius searchlight analysis). Keeping the code and commentary together in working files (e.g., via knitr) helps, but there's often no way around rerunning the entire final analysis pipeline (i.e., starting with preprocessed NIfTIs) to be sure that all the steps actually were performed as described.

UPDATE 1 February 2016: The paper and code are now live.