connectome workbench: view subjects' data

In the previous post I described how to import a nifti image into the Connectome Workbench, as well as how to install and get started with the Workbench. In this post I'll describe how to get and view the Human Connectome Project data, in and out of the Workbench. If you know of easier/more reliable/faster ways to do anything I describe here, please let me know.

getting the data

I found downloading the data from the Connectome database quite straightforward. You need to get an account (and agree to usage terms), but it's all quite fast. The datasets are large, so I suggest you just try one person's data to start. To do so, click the "Download Now" button under the "1 subject" box. It won't actually download right away, but rather take you to a screen where you can specify what exactly you want to download. On the second screen, click the "queue for download" buttons next to each sort of file you want. I suggest you pick the preprocessed structural data (e.g. "HCP Q3 Data Release Structural Preprocessed") and some functional data (e.g. "HCP Q3 Data Release Task Motor Skills fMRI Preprocessed"). The click the "Download Packages" button at the bottom of the page to actually start the download.

I was confused the first time because the files went into Aspera Connect's default directory; on my Windows box I right-click the Aspera icon and select Preferences to see (and change) where it puts the files. This thread on the HCP-Users mailing list (and this documentation) talks about their use of Aspera Connect for the downloading.

figuring out the files: task labels and volumetric data

Once you've got the files downloaded, unzip them to somewhere handy. They'll create a big directory structure, with the top directory called the subject's ID code (e.g. 100307_Q3). If you followed my suggestions above, the functional data will be in /MNINonLinear/Results/tfMRI_MOTOR_LR/ and /MNINonLinear/Results/tfMRI_MOTOR_RL/. Two motor (and most task-type) runs are in the HCP protocol, with _LR and _RL referring to the scanner encoding direction used for each run.

The tasks are described in Barch et al. 2013 (that issue of NeuroImage has several articles with useful details about the HCP protocols and data), and the onset times (in seconds) are given in text files in the EVs subdirectories for each run's data, as well as in larger files (eprime output?) in each run directory (e.g. MOTOR_run2_TAB.txt).

I couldn't find a concise key for the task files, but working back and forth between Barch 2013 and the files I figured out that the first column of each EVs file is the onset time of a block, and the second column the block duration, also in seconds (the TR is 720 msec, so it's easy enough to calculate between TR and seconds). rh.txt is the right hand (actually finger) movement, rf.txt the right foot (toe) movement, t.txt the tongue movement, etc.
UPDATE (19 May 2014): The "tfMRI scripts and data files" section Q3_Release_Reference_Manual.pdf describes this a bit better.

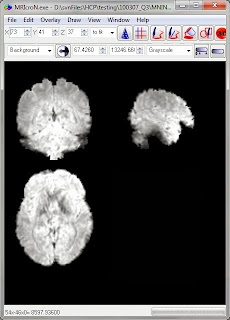
Now that we know the onset times for each task block we can do a volumetric analysis in our usual favorite manner, using the preprocessed .nii.gz files in each run directory (e.g. tfMRI_MOTOR_LR.nii.gz). A full description of the preprocessing is in Glasser et al. 2013; motion correction and spatial normalization (to the MNI template) is included.

These are pretty functional images; this is one of the functional runs.

figuring out the files: surface-based

The HCP data is not just available in volumes, but surfaces as well (actually, a big focus is on surface-type data, see Glasser 2013), and these files need to be opened with Workbench programs. I certainly don't have all of these figured out, so please send along additional tips or corrections if you have them.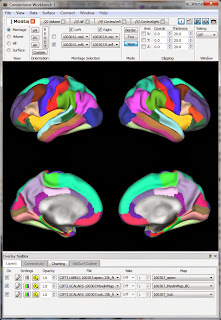

The surface-type functional data is in .dtseries.nii files in each runs' directory (e.g. tfMRI_MOTOR_LR_Atlas.dtseries.nii). As far as I can tell these are not "normal" NIfTI images (despite the .nii suffix) but rather a "CIFTI dense timeseries file". Various wb_command programs can read these files, as well as the Workbench.

So, let's view the functional data in Workbench. My approach is similar to what I described for viewing a NIfTI: first get a blank brain (in this case, the downloaded subject's anatomy), then load in the functional data (in this case, the .dtseries.nii for a motor run). I believe the proper 'blank brain' to use is the one downloaded into the subject's /MNINonLinear/fsaverage_LR32k/ directory; there's only one .spec file in that directory. Opening that .spec file (see the first post for what that means) will bring up a set of labels and surfaces, shown at right.

Now we can open up the functional data. Choose File then Open File in the top Workbench menu, and change the selection to Files of type: "Connectivity - Dense Data Series Files (*.dtseries.nii)". Navigate to the directory for a run and open up the .dtseries.nii (there's just one per run). (aside, the "Connectivity" in the File Type box confuses me; this isn't connectivity data as far as I can tell)

As before, the Workbench screen won't change, but the data should be loaded. Switch to the Charting tab on the bottom of the screen (Overlay ToolBox section), and click the little Graph button to the left of the .dtseries.nii file name (marked with an orange arrow below). Now, if you click somewhere on the brain two windows will appear: one showing the timecourse of the grayordinate you clicked on (read out of the .dtseries.nii) and the usual Information window giving the label information for the grayordinate.

comments

Clicking the Export ... button in the Time Course window will let you save a text file (it says "Dvars Files" but it's plain text) of the time course, but I haven't yet worked out how to extract sets of timecourses, though people are quite helpful on the mailing list. The various .gii and .*.nii files are still rather a black box for me; access appears to be from various wb_command programs.

connectome workbench: plot a NIfTI image

NOTICE (8 February 2018): The material in this post is outdated. I'm leaving it after the jump for archiving, but if you're trying to learn Workbench you should consult this new tutorial for a general introduction, and this one for instructions about creating a surface from a volumetric image.

linear svm behavior: discontinuous information detection

Since starting with MVPA I've struggled with connecting classification accuracy to the properties of the voxels that (as a group) have the accuracy: does the high accuracy mean that all the voxels are informative? Just some of them? How to tell? Even with a linear svm these are not easy questions to answer.

Some of my efforts to figure out what linear SVMs are doing with fMRI data contributed to the examples in my recent paper about searchlight analysis. In this post I'll describe figure 4 in the paper (below); this is in the supplemental as Example 1 (code is example1.R).

The simulated dataset is for just one person, and has a single ROI of 500 voxels, two classes (balanced, so chance is 0.5), and four runs. Classification is with a linear SVM (c=1), averaged over a four-fold cross-validation (partitioning on the runs).

A key for this example is that the 500 voxels were created to be equally informative: the values for each voxel were created by choosing random numbers (from a uniform distribution) for one class' examples, and then adding 0.1 to each value for the examples of the other class. For concreteness, here's Figure 1 from the Supplemental, showing part of the input data:

So, we have 500 voxels, the data for each constructed so that each voxel is equally informative (in the sense of amount of activation difference between the classes). Now, let's classify. As expected, if we classify with all 500 voxels the accuracy is perfect (expected, since we know the classes vary). But what if we use less than all the voxels? I set up the example to classify sequentially larger voxel subsets: each larger subset is made by adding a voxel to the previous subset, so that each subset includes the voxels from all smaller subsets. For example, the two-voxel subset includes voxels 1 and 2, the three-voxel subset has voxels 1, 2, and 3, the four-voxel subset voxels 1, 2, 3, and 4, etc.

Figure 4 in the manuscript (below) shows one happens for one run of the simulation: the number of voxels increases from 1 to 500 along the x-axis, and accuracy from 0.5 (chance) to 1 (perfect) along the y.

In the manuscript I call this an example of discontinuous information detection: the accuracy does not increase smoothly from 0.5 to 1, but rather jumps around. For example, the 42-voxel subset classifies at 0.81. Adding voxels one-at-a-time, we get accuracies of 0.72, 0.75, 0.78, 0.94 ... the accuracy went down abruptly, then back up again. Why? My best guess is that it has to do with the shape of the points in hyperspace; each time we add a voxel we also add a dimension, and so change the point clouds, making it easier (or not) for the linear SVM to separate.

What does this mean in practice? I guess it makes me think of classification accuracies as "slippery": somewhat difficult to grasp and unpredictable, so you need to use extreme caution before thinking that you understand their behavior.

Discontinuous information detection is perhaps also an argument for stability testing. In the Figure 4 run (graph above), the accuracy didn't change much after around 210 voxels: it was consistently very high. It is much easier to interpret our results if we're pretty confident that we're in one of these stable zones. For example, suppose we have an anatomic ROI that classifies well. Now, suppose we add in the border voxels, one at a time, classifying  each "ROI + 1" subset. I'd be a lot more confident that the ROI captured a truly informative set of voxels if the accuracy stayed more-or-less the same as individual voxels were added, than if it had huge variance.

We want to make sure we're on a plateau of high accuracy (robust to minor changes in voxels or processing), not that we happened to land upon a pointy mountain top, such that any tiny variation will send us back to chance. And this example shows that linear SVMs can easily make "pointy mountains" with fMRI data.