An interesting new paper about RSA,
A Toolbox for Representational Similarity Analysis (Nili et al 2014, see citation below), shifted my picture of RSA a bit, making me realize I haven't always used the technique quite properly.
First, as you'd guess from the title, the paper mostly describes
a MATLAB package for performing RSA. I could easily download the package and start looking at the demos and documentation, but there is a lot in the package, and understanding what all it's capable of (and how exactly it's doing everything) is not a job for an hour or two. It certainly looks worth careful examination, though; I'm particularly interested in the statistical inference functions.
The part I mostly want to comment on is separate from the MATLAB package: the paper suggests using a linear discriminant analysis t-value as a
distance (dissimilarity) metric measure of discriminability instead of Pearson correlation (1 - Pearson correlation was suggested in
Kriegeskorte 2008). Here's how they describe the method (there's a bit more in the supplemental):
"We first divide the data into two independent sets. For each pair of stimuli, we then fit a Fisher linear discriminant to one set, project the other set onto that discriminant dimension, and compute the t value reflecting the discriminability between the two stimuli. We call this multivariate separation measure the linear-discriminant t (LD-t) value."
This is dense. To unpack it a bit, the idea is that you're using a statistic derived from a classification analysis for the distance metric. They suggest using Fisher linear discriminant analysis (LDA) for the classification algorithm, with two-fold cross-validation, averaging results across the folds. LDA strikes me as a reasonable suggestion, and I assume any sort of reasonable cross-validation scheme (e.g. leave-one-run-out) would be fine.
But, how to derive the a t-value from the cross-validated LDA? The paper's description wasn't detailed enough for me, so I poked around in the toolbox code, and found the
fishAtestB_optShrinkageCov_C function in
/Engines/fisherDiscrTRDM.m. It looks like they're fitting the discriminant to the training dataset, projecting the test dataset onto the discriminant, then
doing a t-test on the "error variance" computing a t-value from the test data projected on the discriminant. The function code does everything with linear algebra; my MATLAB (and linear algebra) is too rusty for it to all be obvious (e.g. which step, if any, corresponds to the coefficients produced by the R lda command? Is it a two-sided t-test against zero?).
Please comment or email if you can clarify and I'll update this post. See this new post.
Anyway, the idea of using a classification-derived distance metric for RSA is appealing, particularly to get a consistent and predictable zero when stimuli are truly unrelated (fMRI examples are often a bit correlated, making correlation-based RSA comparisons sometimes between "not that correlated" and "somewhat correlated", rather than the more interpretable "nothing" and "something").
Which brings me to what I realized I had wrong about RSA. To do cross-validation, you need multiple examples of the same stimulus, and at the end you have a single number (accuracy, LD-
t, whatever). RSA is accordingly not done between
examples (e.g. individual trials) but between
stimulus types (classes with lots of examples; what we classify).
This RSA matrix (the official term is "RDM") is from
a previous post, which I described as "an RSA matrix for a dataset with six examples in each of two classes (w and f)." While the matrix is sensible (w-f cells are oranger - less correlated - than w-w and f-f cells), the matrix should properly be
a single value: the distance between w and f.
In other words, to make an RSA matrix (RDM) I needed at least
three classes; not multiple examples of
two classes. Say the new class is 'n'. Then, my RSA matrix would have w, f, and n along each axis, and we can ask questions like, "is w is more similar to f or n?". That RSA matrix would have just three numbers: the distances between w and f, w and n, and f and n. If using Pearson correlation, we'd calculate those three numbers by averaging (or some other sort of temporal compression, such as fitting a linear model) across the examples of each class (here, w1, w2, w3, w4, w5, w6) to get one example per class, then correlating these vectors (e.g. w with f). If using LDA, we'd (for example) use the first three w and f examples to train the classifier, then test on the last three of each (and the reverse), then calculate the LD-
t. (To be clear, you can calculate LD-
t with just two classes, it won't really look like an RDM since you just have one value (w-f).)
 Nili H, Wingfield C, Walther A, Su L, Marslen-Wilson W, & Kriegeskorte N (2014). A toolbox for representational similarity analysis. PLoS computational biology, 10 (4) PMID: 24743308
UPDATE 17 July 2014: Changed a bit of the text (strikeouts) in response to helpful comments from Hamed Nili. He also pointed out this page, which describes a few other aspects of the paper and toolbox.
UPDATE 21 August 2014: see this post for a detailed description of how to calculate the LD-t.
Nili H, Wingfield C, Walther A, Su L, Marslen-Wilson W, & Kriegeskorte N (2014). A toolbox for representational similarity analysis. PLoS computational biology, 10 (4) PMID: 24743308
UPDATE 17 July 2014: Changed a bit of the text (strikeouts) in response to helpful comments from Hamed Nili. He also pointed out this page, which describes a few other aspects of the paper and toolbox.
UPDATE 21 August 2014: see this post for a detailed description of how to calculate the LD-t.
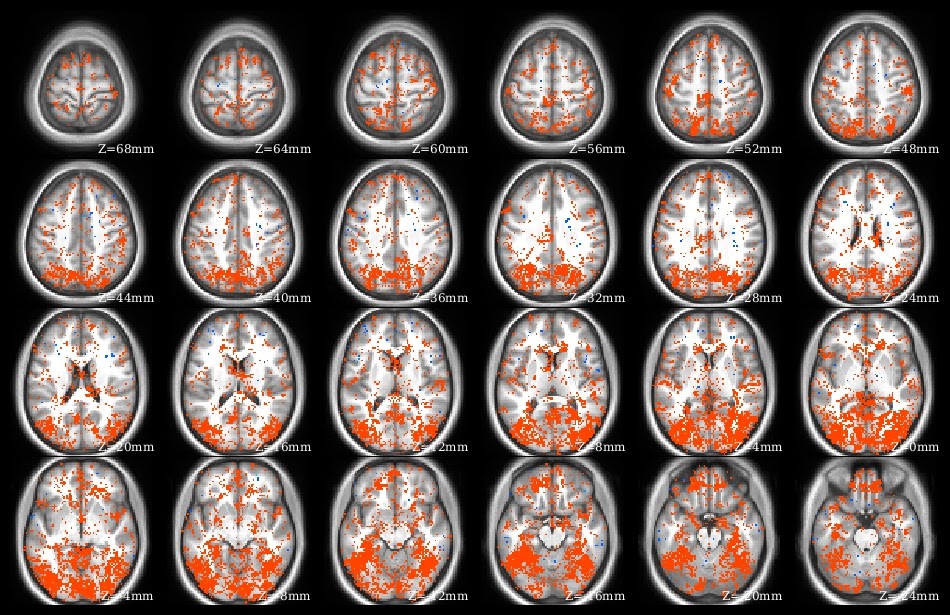 The demo code linked in this post does a voxelwise t-test in R. It takes as input a set of 3d NIfTI files, where each NIfTI is assumed to come from a different person, each voxel of which contains a statistic describing effect strength (for example, accuracy resulting from a searchlight analysis). The code reads the 3d NIfTI images into a 4d array (people in the fourth dimension), then performs a t-test at each voxel, saving the t-values for each voxel in a new NIfTI image. This figure shows the t-value image produced by the demo code.
The demo code linked in this post does a voxelwise t-test in R. It takes as input a set of 3d NIfTI files, where each NIfTI is assumed to come from a different person, each voxel of which contains a statistic describing effect strength (for example, accuracy resulting from a searchlight analysis). The code reads the 3d NIfTI images into a 4d array (people in the fourth dimension), then performs a t-test at each voxel, saving the t-values for each voxel in a new NIfTI image. This figure shows the t-value image produced by the demo code.




